Relations between DST_I and DST_II
Contents
Definitions
Result of transform is y=x*T, where y, x are row-vectors T is transform matrix
DST_I matrix definition
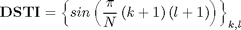
N=8; DST1=sin(pi/N*((0:N-2)+1)'*((0:N-2)+1))
DST1 =
0.3827 0.7071 0.9239 1.0000 0.9239 0.7071 0.3827
0.7071 1.0000 0.7071 0.0000 -0.7071 -1.0000 -0.7071
0.9239 0.7071 -0.3827 -1.0000 -0.3827 0.7071 0.9239
1.0000 0.0000 -1.0000 -0.0000 1.0000 0.0000 -1.0000
0.9239 -0.7071 -0.3827 1.0000 -0.3827 -0.7071 0.9239
0.7071 -1.0000 0.7071 0.0000 -0.7071 1.0000 -0.7071
0.3827 -0.7071 0.9239 -1.0000 0.9239 -0.7071 0.3827
DST_II matrix definition
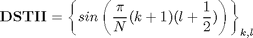
DST2=sin(pi/N*((0:N-1)+1)'*((0:N-1)+1/2))
DST2 =
0.1951 0.5556 0.8315 0.9808 0.9808 0.8315 0.5556 0.1951
0.3827 0.9239 0.9239 0.3827 -0.3827 -0.9239 -0.9239 -0.3827
0.5556 0.9808 0.1951 -0.8315 -0.8315 0.1951 0.9808 0.5556
0.7071 0.7071 -0.7071 -0.7071 0.7071 0.7071 -0.7071 -0.7071
0.8315 0.1951 -0.9808 0.5556 0.5556 -0.9808 0.1951 0.8315
0.9239 -0.3827 -0.3827 0.9239 -0.9239 0.3827 0.3827 -0.9239
0.9808 -0.8315 0.5556 -0.1951 -0.1951 0.5556 -0.8315 0.9808
1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000
Finding relations
From [1] we know that DSTI matrix can be expressed in terms of Tschebyshev polynomials
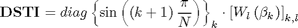
where
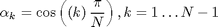
are roots of polynomial
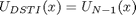
DSTII matrix can be analogously expressed as
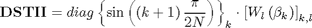
where
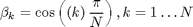
are roots of polynomial
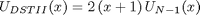
Because there exist relation
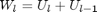
and
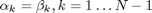
we can express DSTII through DSTI
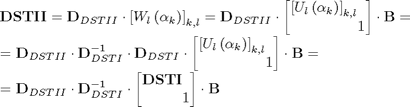
where
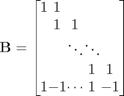
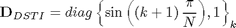
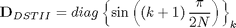
B=diag(ones(1,N))+diag(ones(1,N-1),1); B(end,:)=(-1).^(0:N-1); D1=diag([sin(pi/N*((0:N-2)+1)), 1]); D2=diag(sin(pi/2/N*((0:N-1)+1)));
Check expression of DST_I through DST_II
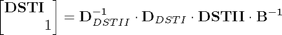
inv(D2)*D1*DST2*inv(B)
ans =
0.3827 0.7071 0.9239 1.0000 0.9239 0.7071 0.3827 -0.0000
0.7071 1.0000 0.7071 0.0000 -0.7071 -1.0000 -0.7071 0.0000
0.9239 0.7071 -0.3827 -1.0000 -0.3827 0.7071 0.9239 -0.0000
1.0000 0.0000 -1.0000 -0.0000 1.0000 0.0000 -1.0000 -0.0000
0.9239 -0.7071 -0.3827 1.0000 -0.3827 -0.7071 0.9239 -0.0000
0.7071 -1.0000 0.7071 0.0000 -0.7071 1.0000 -0.7071 0.0000
0.3827 -0.7071 0.9239 -1.0000 0.9239 -0.7071 0.3827 -0.0000
0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 1.0000
Check computation of DSTI transform
x=randn(1,N-1) y=x*DST1 % true result y1=[x 0]*inv(D2)*D1*DST2*inv(B) % compute DSTI using DSTII transform
x =
0.2120 0.2379 -1.0078 -0.7420 1.0823 -0.1315 0.3899
y =
-0.3676 -1.2343 1.3448 1.9122 -0.2897 -1.9730 0.9660
y1 =
-0.3676 -1.2343 1.3448 1.9122 -0.2897 -1.9730 0.9660 -0.0000
Check expression of DST_II through DST_I
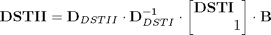
DST1a=eye(N);DST1a(1:end-1,1:end-1)=DST1; D2*inv(D1)*DST1a*B
ans =
0.1951 0.5556 0.8315 0.9808 0.9808 0.8315 0.5556 0.1951
0.3827 0.9239 0.9239 0.3827 -0.3827 -0.9239 -0.9239 -0.3827
0.5556 0.9808 0.1951 -0.8315 -0.8315 0.1951 0.9808 0.5556
0.7071 0.7071 -0.7071 -0.7071 0.7071 0.7071 -0.7071 -0.7071
0.8315 0.1951 -0.9808 0.5556 0.5556 -0.9808 0.1951 0.8315
0.9239 -0.3827 -0.3827 0.9239 -0.9239 0.3827 0.3827 -0.9239
0.9808 -0.8315 0.5556 -0.1951 -0.1951 0.5556 -0.8315 0.9808
1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000 1.0000 -1.0000
Check computation of DSTII transform
x=randn(1,N) y=x*DST2 % true result y1=x*D2*inv(D1)*DST1a*B % compute DSTII using DSTI transform
x =
0.0880 -0.6355 -0.5596 0.4437 -0.9499 0.7812 0.5690 -0.8217
y =
-0.5550 -0.9089 -0.8097 0.8994 -1.0737 3.2332 -1.4077 -0.4960
y1 =
-0.5550 -0.9089 -0.8097 0.8994 -1.0737 3.2332 -1.4077 -0.4960
Reference
[1] Markus Pueschel, Jose M.F. Moura. The Algebraic Approach to the Discrete Cosine and Sine Transforms and their Fast Algorithms SIAM Journal of Computing 2003, Vol. 32, No. 5, pp. 1280-1316.