Relations between DCTV and DSTVI

Contents

Definitions

Transform matrix is defined for operating on column-vectors y=T*x, where y, x are column-vectors, T is transform matrix

DCTV matrix definition

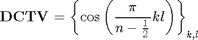
$${\bf DCTV}={\left\{{\cos\left({{{\pi}\over{n-{{1}\over{2}}}}kl}\right)}\right\}}_{k,l}$$

N1=9; N=N1;
k=0:N1-1;  l=0:N1-1;
DCT5=cos(pi/(N-1/2)*k'*l)       % display DCTV matrix

DCT5 =
  Columns 1 through 7
    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000
    1.0000    0.9325    0.7390    0.4457    0.0923   -0.2737   -0.6026
    1.0000    0.7390    0.0923   -0.6026   -0.9830   -0.8502   -0.2737
    1.0000    0.4457   -0.6026   -0.9830   -0.2737    0.7390    0.9325
    1.0000    0.0923   -0.9830   -0.2737    0.9325    0.4457   -0.8502
    1.0000   -0.2737   -0.8502    0.7390    0.4457   -0.9830    0.0923
    1.0000   -0.6026   -0.2737    0.9325   -0.8502    0.0923    0.7390
    1.0000   -0.8502    0.4457    0.0923   -0.6026    0.9325   -0.9830
    1.0000   -0.9830    0.9325   -0.8502    0.7390   -0.6026    0.4457
  Columns 8 through 9
    1.0000    1.0000
   -0.8502   -0.9830
    0.4457    0.9325
    0.0923   -0.8502
   -0.6026    0.7390
    0.9325   -0.6026
   -0.9830    0.4457
    0.7390   -0.2737
   -0.2737    0.0923

DCTV in terms of Tschebyshev polynomials

The DCTV matrix can be expressed in terms of Tschebyshev polynomials [1]

$${\mathbf {DCTV}} = \left[ {T_l \left( {\alpha _k } \right)} \right]_{k,l} $$

where

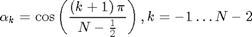
$${\rm \alpha}_{k}=\cos\left({{{\left({k+1}\right){\rm \pi}}\over{N-{{1}\over{2}}}}}\right),k=-1\ldots N-2$$

are roots of polynomial

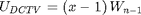
$$U_{DCTV}=\left({x-1}\right)W_{n-1}$$

alpha=sort([roots(TschebyshevW(N-1)); 1],'descend');
DCT5t=zeros(N1);
for l=0:N1-1,
    DCT5t(:,l+1)=polyval(TschebyshevT(l),alpha)';
end
Da5=diag(cos(0*pi/(N-1/2)*k));
DCT5t=Da5*DCT5t                    % display DCTV matrix

% compare DCT5 and DCT5t matrices (show that both definitions above are equivalent)
max(max(abs(DCT5-DCT5t)))

DCT5t =
  Columns 1 through 7
    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000
    1.0000    0.9325    0.7390    0.4457    0.0923   -0.2737   -0.6026
    1.0000    0.7390    0.0923   -0.6026   -0.9830   -0.8502   -0.2737
    1.0000    0.4457   -0.6026   -0.9830   -0.2737    0.7390    0.9325
    1.0000    0.0923   -0.9830   -0.2737    0.9325    0.4457   -0.8502
    1.0000   -0.2737   -0.8502    0.7390    0.4457   -0.9830    0.0923
    1.0000   -0.6026   -0.2737    0.9325   -0.8502    0.0923    0.7390
    1.0000   -0.8502    0.4457    0.0923   -0.6026    0.9325   -0.9830
    1.0000   -0.9830    0.9325   -0.8502    0.7390   -0.6026    0.4457
  Columns 8 through 9
    1.0000    1.0000
   -0.8502   -0.9830
    0.4457    0.9325
    0.0923   -0.8502
   -0.6026    0.7390
    0.9325   -0.6026
   -0.9830    0.4457
    0.7390   -0.2737
   -0.2737    0.0923
ans =
   2.5746e-13

DSTVI matrix definition

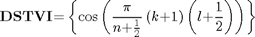
$$ {\mathbf{DSTVI}}\mathrm{{=}}\left\{{\cos\left({\frac{\mathit{\pi}}{{n}\mathrm{{+}}\frac{1}{2}}\left({{k}\mathrm{{+}}{1}}\right)\left({{l}\mathrm{{+}}\frac{1}{2}}\right)}\right)}\right\} $$

N2=8; N=N2;
k=0:N2-1;  l=0:N2-1;
DST6=sin(pi/(N+1/2)*(k+1)'*(l+1/2))       % display DCTV matrix

DST6 =
  Columns 1 through 7
    0.1837    0.5264    0.7980    0.9618    0.9957    0.8952    0.6737
    0.3612    0.8952    0.9618    0.5264   -0.1837   -0.7980   -0.9957
    0.5264    0.9957    0.3612   -0.6737   -0.9618   -0.1837    0.7980
    0.6737    0.7980   -0.5264   -0.8952    0.3612    0.9618   -0.1837
    0.7980    0.3612   -0.9957    0.1837    0.8952   -0.6737   -0.5264
    0.8952   -0.1837   -0.6737    0.9957   -0.5264   -0.3612    0.9618
    0.9618   -0.6737    0.1837    0.3612   -0.7980    0.9957   -0.8952
    0.9957   -0.9618    0.8952   -0.7980    0.6737   -0.5264    0.3612
  Column 8
    0.3612
   -0.6737
    0.8952
   -0.9957
    0.9618
   -0.7980
    0.5264
   -0.1837

DSTVI in terms of Tschebyshev polynomials

The DSTVI matrix can be expressed in terms of Tschebyshev polynomials [1]

$$ {\mathbf{DSTVI}}\mathrm{{=}}{\mathrm{\left[{{W}_{l}\left({{\mathit{\beta}}_{k}}\right)}\right]}}_{k\mathrm{,}l} $$

where

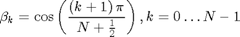
$${\rm \beta}_{k}=\cos\left({{{\left({k+1}\right){\rm \pi}}\over{N+{{1}\over{2}}}}}\right),k=0\ldots N-1 $$

are roots of polynomial

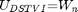
$${U}_{DSTVI}\mathrm{{=}}{W}_{n}$$

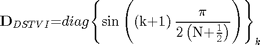
$${\mathbf{D}}_{DSTVI}\mathrm{{=}}{diag}{\mathrm{\left\{{\sin\left({\left({{k}{+}{1}}\right)\frac{\mathrm{\pi}}{{2}\left({{N}{+}\frac{1}{2}}\right)}}\right)}\right\}}}_{k}$$

beta=sort([roots(TschebyshevW(N))],'descend');
DST6t=zeros(N);
for l=0:N2-1,
    DST6t(:,l+1)=polyval(TschebyshevW(l),beta)';
end
Db6=diag(sin(1/2*pi/(N+1/2)*(k+1)));
DST6t=Db6*DST6t                    % display DCTV matrix

% compare DST6 and DST6t matrices (show that both definitions above are equivalent)
max(max(abs(DST6-DST6t)))

DST6t =
  Columns 1 through 7
    0.1837    0.5264    0.7980    0.9618    0.9957    0.8952    0.6737
    0.3612    0.8952    0.9618    0.5264   -0.1837   -0.7980   -0.9957
    0.5264    0.9957    0.3612   -0.6737   -0.9618   -0.1837    0.7980
    0.6737    0.7980   -0.5264   -0.8952    0.3612    0.9618   -0.1837
    0.7980    0.3612   -0.9957    0.1837    0.8952   -0.6737   -0.5264
    0.8952   -0.1837   -0.6737    0.9957   -0.5264   -0.3612    0.9618
    0.9618   -0.6737    0.1837    0.3612   -0.7980    0.9957   -0.8952
    0.9957   -0.9618    0.8952   -0.7980    0.6737   -0.5264    0.3612
  Column 8
    0.3612
   -0.6737
    0.8952
   -0.9957
    0.9618
   -0.7980
    0.5264
   -0.1837
ans =
   2.3470e-13

Finding relations

Because there exist relation

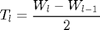
$$ T_l = \frac{{W_l - W_{l - 1} }}{2} $$

and

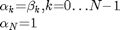
$$ \begin{array}{l} {{\mathrm{\alpha}}_{k}\mathrm{{=}}{\mathrm{\beta}}_{k}{\mathrm{,}}{k}\mathrm{{=}}{0}\mathrm{\ldots}{N}\mathrm{{-}}{1}}\\ {{\mathrm{\alpha}}_{N}\mathrm{{=}}{1}} \end{array} $$

we can express DCTV through DSTVI

$$ \begin{array}{l} {{\mathbf{DCTV}}\mathrm{{=}}{\mathrm{\left[{{T}_{l}\left({{\mathrm{\alpha}}_{k}}\right)}\right]}}_{k\mathrm{,}l}\mathrm{{=}}{\mathrm{\left[{\begin{array}{cc}{1}&{}\\{}&{{W}_{l}\left({{\mathrm{\beta}}_{k}}\right)}\end{array}}\right]}}_{k\mathrm{,}l}\mathit{\cdot}{\mathbf{B}}\mathrm{{=}}\left[{\begin{array}{cc}{1}&{}\\{}&{{\left({{\mathbf{D}}_{DSTVI}}\right)}^{\mathrm{{-}}{1}}\mathit{\cdot}{\mathbf{D}}_{DSTVI}\mathit{\cdot}{\left[{{W}_{l}\left({{\mathit{\beta}}_{k}}\right)}\right]}_{k\mathrm{,}l}}\end{array}}\right]\mathit{\cdot}{\mathbf{B}}\mathrm{{=}}}\\ {\mathrm{{=}}\left[{\begin{array}{cc}{1}&{}\\{}&{{\left({{\mathbf{D}}_{DSTVI}}\right)}^{\mathrm{{-}}{1}}\mathrm{\cdot}{\mathbf{DSTVI}}}\end{array}}\right]\mathrm{\cdot}{\mathbf{B}}} \end{array} $$

where

$${\mathbf{B}}\mathrm{{=}}\mathrm{\frac{1}{2}}\mathrm{\left[{\begin{array}{cccccc}{2}&{2}&{2}&{\cdots}&{2}&{2}\\{2}&{{-}{1}}&{}&{}&{}&{}\\{}&{1}&{{-}{1}}&{}&{}&{}\\{}&{}&{1}&{\ddots}&{}&{}\\{}&{}&{}&{\ddots}&{{-}{1}}&{}\\{}&{}&{}&{}&{1}&{{-}{1}}\end{array}}\right]}$$

B=toeplitz([0.5 zeros(1,N-1)]',[0.5        -0.5 zeros(1,N-length([0.5        -0.5]))]);
B(1,1)=1;
B=[B [0; B(1:end-1,end)]];
B=[ones(1,size(B,2)); B];

Check expression of DCTV through DSTVI

$${\mathbf{DCTV}}\mathrm{{=}}\mathrm{\left[{\begin{array}{cc}{1}&{}\\{}&{{\left({{\mathbf{D}}_{DSTVI}}\right)}^{{-}{1}}\cdot{\mathbf{DSTVI}}}\end{array}}\right]}\mathrm{\cdot}{\mathbf{B}}$$

DCT5a=Da5*blkdiag(1,inv(Db6)*DST6)*B
% compare DCT5 and DCT5a matrices (show correctness of representation of DCTV through DSTVI)
max(max(abs(DCT5-DCT5a)))

DCT5a =
  Columns 1 through 7
    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000    1.0000
    1.0000    0.9325    0.7390    0.4457    0.0923   -0.2737   -0.6026
    1.0000    0.7390    0.0923   -0.6026   -0.9830   -0.8502   -0.2737
    1.0000    0.4457   -0.6026   -0.9830   -0.2737    0.7390    0.9325
    1.0000    0.0923   -0.9830   -0.2737    0.9325    0.4457   -0.8502
    1.0000   -0.2737   -0.8502    0.7390    0.4457   -0.9830    0.0923
    1.0000   -0.6026   -0.2737    0.9325   -0.8502    0.0923    0.7390
    1.0000   -0.8502    0.4457    0.0923   -0.6026    0.9325   -0.9830
    1.0000   -0.9830    0.9325   -0.8502    0.7390   -0.6026    0.4457
  Columns 8 through 9
    1.0000    1.0000
   -0.8502   -0.9830
    0.4457    0.9325
    0.0923   -0.8502
   -0.6026    0.7390
    0.9325   -0.6026
   -0.9830    0.4457
    0.7390   -0.2737
   -0.2737    0.0923
ans =
   1.6653e-15

Check expression of DSTVI through DCTV

$$\left[{\begin{array}{cc}{1}&{}\\{}&{\mathbf{DSTVI}}\end{array}}\right]\mathrm{{=}}\mathrm{\left[{\begin{array}{cc}{1}&{}\\{}&{{\mathbf{D}}_{DSTVI}}\end{array}}\right]}\mathrm{\cdot}{\mathbf{DCTV}}\mathrm{\cdot}{\mathbf{B}}^{\mathrm{{-}}{1}}$$

DST6a=blkdiag(1,Db6)*inv(Da5)*DCT5*inv(B);
DST6a=DST6a(2:end,2:end)
% compare DST6 and DST6a matrices (show correctness of representation of DSTVI through DCTV)
max(max(abs(DST6-DST6a)))

DST6a =
  Columns 1 through 7
    0.1837    0.5264    0.7980    0.9618    0.9957    0.8952    0.6737
    0.3612    0.8952    0.9618    0.5264   -0.1837   -0.7980   -0.9957
    0.5264    0.9957    0.3612   -0.6737   -0.9618   -0.1837    0.7980
    0.6737    0.7980   -0.5264   -0.8952    0.3612    0.9618   -0.1837
    0.7980    0.3612   -0.9957    0.1837    0.8952   -0.6737   -0.5264
    0.8952   -0.1837   -0.6737    0.9957   -0.5264   -0.3612    0.9618
    0.9618   -0.6737    0.1837    0.3612   -0.7980    0.9957   -0.8952
    0.9957   -0.9618    0.8952   -0.7980    0.6737   -0.5264    0.3612
  Column 8
    0.3612
   -0.6737
    0.8952
   -0.9957
    0.9618
   -0.7980
    0.5264
   -0.1837
ans =
   3.1086e-15

Check computation of DCTV transform

x=randn(N1,1);
disp('x''=');disp(x');
y=DCT5*x;                      % true result
disp('y''=');disp(y');
y1=Da5*blkdiag(1,inv(Db6)*DST6)*B*x;            % compute DCTV using DSTVI transform
disp('y1''=');disp(y1');

x'=
  Columns 1 through 7
   -0.8095   -2.9443    1.4384    0.3252   -0.7549    1.3703   -1.7115
  Columns 8 through 9
   -0.1022   -0.2414
y'=
  Columns 1 through 7
   -3.4300   -1.4360   -3.2739   -3.4892   -1.3389   -2.7776    0.3708
  Columns 8 through 9
    5.7705    1.0085
y1'=
  Columns 1 through 7
   -3.4300   -1.4360   -3.2739   -3.4892   -1.3389   -2.7776    0.3708
  Columns 8 through 9
    5.7705    1.0085

Check computation of DSTVI transform

x=randn(N2,1);
disp('x''=');disp(x');
y=DST6*x;                      % true result
disp('y''=');disp(y');
y1=blkdiag(1,Db6)*inv(Da5)*DCT5*inv(B)*[0;x];            % compute DSTVI using DCTV transform
disp('y1''=');disp(y1');
% Reference

x'=
  Columns 1 through 7
    0.3192    0.3129   -0.8649   -0.0301   -0.1649    0.6277    1.0933
  Column 8
    1.1093
y'=
  Columns 1 through 7
    1.0392   -2.7589    2.0960    0.1857    1.1443    0.8074    0.2884
  Column 8
   -0.9837
y1'=
  Columns 1 through 7
    0.0000    1.0392   -2.7589    2.0960    0.1857    1.1443    0.8074
  Columns 8 through 9
    0.2884   -0.9837


Published with MATLAB® 7.14